Cuando hablamos de Big Data y Aprendizaje Automático en Salud, las técnicas que se suelen utilizar para analizar y predecir información están en su mayoría diseñadas para datos estáticos, como pueden ser la edad de un individuo, su sexo, la presencia de comorbilidades o la renta media del barrio en el que vive. Sin embargo, es frecuente que la información tenga formato de serie temporal, es decir, una sucesión de datos medidos y ordenados a lo largo del tiempo, como los que recogen algunos dispositivos médicos.
En estos casos, resulta interesante tener en cuenta el contexto histórico de las variables para predecir su comportamiento futuro. En medicina, puesto que la mayoría de fenómenos dependen de una serie de eventos pasados, es útil gestionar estos datos dinámicos, ya sea para el control de epidemias, la implantación de sistemas de alertas tempranas de ciertas enfermedades o para la fabricación de prótesis inteligentes a partir de señales nerviosas.
Hacer un análisis descriptivo o predictivo tradicional cuando los datos son series temporales supone distintas limitaciones, como una dimensionalidad demasiado grande si se utiliza cada marca de tiempo como una variable o problemas de creación de conjuntos de datos cuando las series temporales no tienen la misma longitud.
Por lo tanto, en este artículo detallaremos las distintas herramientas específicas para el procesamiento de estos datos, junto con algunos ejemplos del ámbito de la salud. Además, en una segunda parte, nos centraremos en el desarrollo de modelos de predicción de series temporales.
Si estás leyendo este post, te interesa leer también
Análisis de series temporales en salud
El análisis de datos de series temporales requiere tener en cuenta ciertas consideraciones que tienen que ver, por ejemplo, con su regularidad. No obstante, una vez resuelto esto, se pueden hacer una serie de mediciones más o menos simples para describir estos datos dinámicos y analizar sus características y su comportamiento.
Muestreo de series temporales en salud
En el ámbito biosanitario, una buena práctica para el tratamiento de los datos temporales es entender sus características mediante distintos métodos de análisis descriptivo, ya sea para extraer conclusiones médicas directamente o para saber cuál es la mejor manera de enfocar la predicción.
Para las técnicas analíticas y predictivas que se describen en este artículo, es conveniente que los intervalos de tiempo entre cada dato de la serie temporal y el siguiente sean constantes. Cuando los datos corresponden a una señal fisiológica recogida con algún tipo de dispositivo medidor, como pueden ser las señales nerviosas musculares grabadas durante una electromiografía, las muestras suelen estar separadas por intervalos de tiempo regulares.
Sin embargo, con frecuencia, las series temporales que se estudian tienen marcas de tiempo irregulares, como por ejemplo las mediciones manuales de temperatura que se realizan a los pacientes ingresados. En estos casos, se deben interpolar los datos, ya sea linealmente o con métodos más sofisticados (polinomialmente, con funciones Spline, etc.), para poder definir una frecuencia de muestreo. Además, también es preferible que cuando se dispone de varias series temporales cuyas interacciones se van a examinar (p.e. concentraciones de oxígeno y bióxido de carbono en sangre a lo largo del día), todas tengan datos en las mismas marcas de tiempo.
Mediciones simples de series temporales: media y varianza
Aparte de representar una serie temporal para intuir sus características, las mediciones más simples que podemos realizar con estos datos son la media y la varianza en función del tiempo. Por ejemplo, podemos calcular la media y varianza por horas de las señales diarias de glucosa en sangre de un paciente para comprobar si la glucosa tiende a ser más alta o más volátil por las tardes que por las mañanas.
También podemos utilizar otros cálculos estadísticos como es la función de densidad de probabilidad para obtener información, ya sea para la serie temporal entera o para la serie temporal en un momento dado del tiempo. Por ejemplo, podríamos usarla para estimar la probabilidad de que la glucosa en sangre del paciente esté entre 170 y 180 mg/dL a las 11:00 h. de la mañana.
Funciones de correlación de series temporales
Unas técnicas muy potentes para comprender el comportamiento de nuestras series temporales son las funciones de correlación. En esta sección repasaremos tres: la función de autocorrelación simple, la función de autocorrelación parcial, y la función de correlación cruzada.
La primera, la función de autocorrelación, muestra la correlación de una señal consigo misma a pasado (o a futuro, ya que es simétrica). En concreto, muestra la correlación entre la señal y la misma señal ? intervalos de tiempo antes, por lo que es una función de ?.
Aquí vemos que es importante que las muestras de la serie temporal se recojan regularmente, puesto que la función se expresa en número de intervalos de tiempo. Por ejemplo, pongamos que una señal de glucosa se muestrea cada 5 minutos y que la función de correlación muestra un pico en ? = 12. Esto nos indicaría que la glucosa en sangre está correlacionada consigo misma 12 x 5 minutos = 60 minutos a pasado, o sea que, si en un momento la glucosa aumenta, también tiende a aumentar una hora después (por simetría) y si la glucosa disminuye, también tiende a disminuir una hora después.
Por otro lado, la función de autocorrelación parcial (PACF) también calcula la correlación de una señal consigo misma ? intervalos de tiempo antes, esta vez suprimiendo en el cálculo los efectos de las correlaciones de la señal consigo misma 1, 2, … ?-1 intervalos de tiempo antes. Esta función no da información fácilmente interpretable en un análisis descriptivo, pero es muy útil para la creación de una variedad de modelos clásicos de predicción de series temporales. Veremos algunos de ellos en las siguientes secciones.
Finalmente, podemos utilizar la función de correlación cruzada para analizar la correlación entre dos series temporales distintas a pasado y a futuro. Explicaremos esto con un ejemplo:
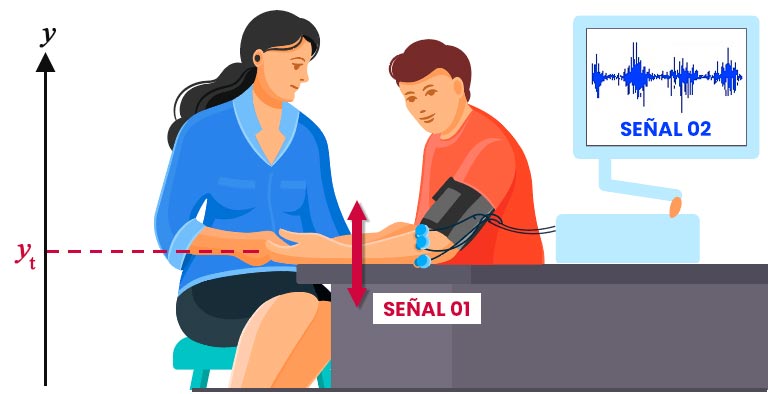
Generamos un experimento en el que un sujeto debe mover el brazo en un eje vertical y medimos dos variables cada 0.1 segundos: la posición de la mano y las señales nerviosas de los músculos del antebrazo. Queremos entender cómo varía cada una de estas señales respecto a la otra, por lo que calculamos y dibujamos la función de correlación cruzada entre la posición vertical de la mano y la actividad nerviosa del brazo. Encontramos un pico positivo en ? = -5 y un pico negativo en ? = 10. Recordando que esta función no es simétrica, el pico positivo en ? = -5 nos indica que, cuando la posición de la mano aumenta, la actividad nerviosa del brazo tiende a haber aumentado 5 x 0.1 = 0.5 segundos antes (y viceversa si la posición disminuye). Por otro lado, el pico negativo en ? = 10 nos permite concluir que, cuando la posición de la mano aumenta, la actividad nerviosa tiende a disminuir 10 x 0.1 = 1 segundo más tarde.
Transformada de Fourier para analizar las frecuencias de una serie temporal
Otra herramienta muy útil a la hora de comprender una serie temporal es el análisis de frecuencia obtenido a partir de la Transformada de Fourier (Fourier Transform, FT). Toda señal se puede considerar una combinación de sinusoides de distinta frecuencia, amplitud y fase.
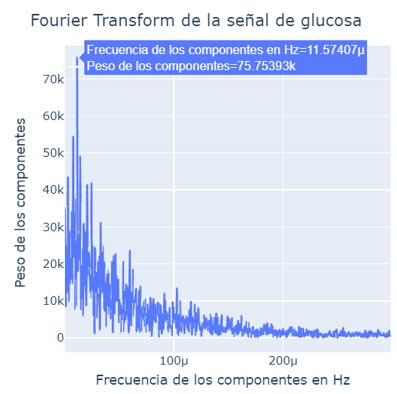Con la FT, descomponemos una serie temporal en estas sinusoides, calculamos sus “energías” (a partir de la amplitud y la fase), y dibujamos en un gráfico el resultado: en el eje X se muestran las frecuencias de los componentes y el en eje Y sus energías. Por lo tanto, con esta técnica podemos averiguar qué frecuencias tienen más peso en una serie temporal.
Al observar la FT de la serie temporal de la glucosa en sangre de un paciente recogida durante 15 días, el pico más alto se encuentra para el componente de frecuencia » 1.15e-5 Hz, que en días corresponde aproximadamente a 1. De esto podemos concluir que la evolución de la glucosa en sangre para el paciente estudiado sigue un patrón de periodicidad principalmente diario.
De la Transformada de Fourier derivan otros métodos de análisis de frecuencia como el Periodograma o el Espectrograma, muy ventajosos para datos longitudinales (distintas observaciones del mismo proceso temporal).
Procesamiento y limpieza de series temporales en salud
Si queremos dar un paso más y desarrollar modelos de predicción a partir de series temporales, debemos someter los datos a un procesamiento y limpieza antes de ser utilizados, para asegurar la calidad de los resultados. A continuación, detallamos algunas técnicas que nos permitirán descartar el ruido o conseguir series temporales estacionarias en biomedicina.
Suavización y filtrado de los datos temporales en salud
En biomedicina, los sensores y otros dispositivos suelen tener errores de medición, como especifican los fabricantes, por lo que nuestras señales temporales muy probablemente contengan ruido. Por ejemplo, en las especificaciones de un termómetro normal de farmacia se suele encontrar un error de ±0.1Cº. Existen varias técnicas para intentar descartar este ruido y suavizar una serie temporal.
Los filtros de Media Móvil son una manera sencilla de eliminar las fluctuaciones a corto plazo de una señal. Consisten en transformar la serie temporal haciendo que cada dato ahora sea una media (posiblemente ponderada) del dato y los X datos anteriores.
Por otro lado, también se puede suprimir el ruido en una serie temporal con un filtro de paso bajo (Low-Pass Filter). Recordando (ver sección anterior) que una señal se puede descomponer en sinusoides de distinta frecuencia y potencia, un filtro de paso bajo mantiene los componentes de una señal cuya frecuencia sea más baja que una frecuencia de corte definida. Para esto es muy útil la información espectral que aporta la Transformada de Fourier. Por tanto, podemos descartar el ruido de la serie descartando los componentes de frecuencias altas.
Además de los de paso bajo, también existen los filtros de paso alto (High-Pass), que conservan los componentes de una señal con frecuencia más alta que la de corte. Pongamos que tenemos datos de un seguimiento semanal del Índice de Masa Corporal (IMC) de un paciente. Observamos que, en los meses fríos del año, el individuo suele engordar y su IMC es, de media, más alto que en los meses cálidos. Con un filtro de paso alto podríamos conservar las fluctuaciones de alta frecuencia para poder analizar las variaciones semanales de IMC sin que se vean afectadas por este patrón bianual en los datos.
Finalmente, los filtros de paso bajo y de paso alto se pueden combinar para crear filtros de paso de banda (Band-Pass) en los que se descartan las frecuencias más bajas y las más altas, o filtros de rechazo de banda (Band-Stop) en los que se eliminan las frecuencias dentro de cierto intervalo.
Estacionarización de series temporales en salud
Varias de las herramientas de predicción que describiremos en las próximas secciones proporcionan mejores resultados cuando las series temporales son estacionarias. La estacionariedad de una serie temporal se establece cuando su media, su varianza y su covarianza son constantes a lo largo del tiempo.
Estas condiciones no se suelen cumplir en las series temporales con las que trabajamos en el campo sanitario, por lo que muchas veces deberemos aplicar transformaciones a nuestros datos para estacionarizarlos, realizar las predicciones e invertir las transformaciones de nuevo.
Estas transformaciones para que la media y la varianza sean constantes son específicas a cada serie temporal, por lo que se deben escoger una vez realizado un análisis descriptivo. Pueden realizarse una diferenciación (diferencia entre un valor de la serie y el valor anterior), un ajuste de funciones, transformaciones lineales o logarítmicas, filtros de paso alto, etc.
En el Instituto de Ingeniería del Conocimiento (IIC), somos expertos en este proceso de preparación de los datos, esencial para desarrollar cualquier proyecto de análisis o de Inteligencia Artificial. En salud, nos adaptamos además a las particularidades de la información y a la privacidad y ética que se requiere para tratarla, asegurando resultados de calidad para mejorar la atención al paciente.
