Los data scientists de la empresa Peter&Wolf Inc tienen el encargo de construir un modelo de clasificación de imágenes para distinguir lobos de perros. El modelo debe recibir fotografías y decir si lo que aparece en ellas es un lobo. Pasado un tiempo, los data scientists, muy orgullosos, presentan sus resultados a Peter, el CEO de la empresa:

Fuente: Explaining Black-Box Machine Learning Predictions – Sameer Singh.

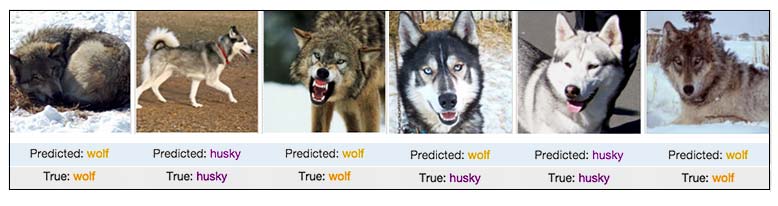
Parece que el modelo no lo hace mal del todo, porque sólo se ha confundido en uno de los 6 casos. El CEO felicita a los empleados y, sin más, ponen el modelo en producción. Los clientes de la empresa pueden subir sus propias fotografías a la web y el modelo devuelve sus predicciones. Para sorpresa de todos, empiezan a recibir feedback negativo del modelo, puesto que, al parecer, falla más de lo esperado. ¿Qué ha pasado?

Se les ocurre obtener explicaciones para su algoritmo, y obtienen los siguientes resultados:

Fuente:  Explaining Black-Box Machine Learning Predictions – Sameer Singh.

En las imágenes de arriba, vemos en qué partes de cada una de las fotografías se ha fijado el modelo para dar sus predicciones. En general, los data scientists se dan cuenta de que el modelo quizá no es tan bueno como parecía, porque casi nunca se fija en el animal en sí, y, si lo hace, mira partes que quizá no son las más adecuadas para distinguir lobos de perros, como, por ejemplo, el lomo o las patas.

Uno de ellos va más allá y mira las explicaciones de las fotos donde la predicción es ‘lobo’ y cae en la cuenta de que ¡el modelo sólo se ha fijado en el fondo! Parece que lo único que hace el modelo es buscar nieve en la fotografía: si hay nieve, predice ‘lobo’, y si no, predice ‘husky’.

¿Por qué la explicabilidad algorítmica es tan importante?

Como pasó en el ejemplo de arriba, en muchas situaciones, conocer no sólo las predicciones de un modelo, sino también el porqué de estas, puede ser útil para entender mejor el problema, los datos e incluso los motivos por los que podría fallar. De hecho, un modelo de machine learning sólo se puede revisar y debuggear si se interpreta.

Por supuesto, la importancia de conocer el porqué de una predicción, de la explicabilidad del algoritmo, depende de las consecuencias que tenga que el modelo cometa un error. Para la empresa ficticia de la historia, este error podría suponer una pérdida de credibilidad para sus clientes, y también pérdidas económicas. Si este modelo lo hubiese construido uno de los empleados de la empresa en su casa para entretenerse, los errores no habrían tenido tanta relevancia. Y, desde luego, si en lugar de ser un modelo que detecta lobos para una aplicación web fuese un algoritmo de detección de ciclistas para un coche autónomo, no se toleraría ningún error.

Otro motivo es la detección de sesgos. Un modelo bien construido reproduce la realidad representada en los datos. Si esos datos tienen algún sesgo indeseado, el modelo lo puede reproducir.  Eso es lo que ocurrió, por ejemplo, con este modelo, que devuelve el riesgo de que la persona de la fotografía vuelva a cometer un delito y que se inclinaba por las personas negras, y también con el modelo de selección de personal descrito en esta noticia y que prefería a los hombres. Las técnicas de explicabilidad nos pueden ayudar a identificar si alguno de estos sesgos no deseados se ha trasladado al modelo y, por tanto, nos pueden servir para corregirlos.

¿Por qué no recurrimos entonces a modelos sencillos? En algunas ocasiones, sería recomendable abandonar los modelos de machine learning por completo y emplear algoritmos deterministas basados en reglas dadas por el conocimiento del negocio o simplemente por legislación, como se muestra en este artículo. En otras, bien por obligación o por comodidad, uno recurre a un modelo más sencillo e interpretable. Ahora bien, estos modelos suelen ser mucho menos expresivos, lo que resulta en un nivel de acierto menor.

eXplainable Artificial Intelligence (XAI): el algoritmo SHAP

Por estos motivos ha surgido un nuevo campo en la Inteligencia Artificial, la XAI (eXplainable Artificial Intelligence), que pretende producir algoritmos que sean tanto potentes como explicables. Esta rama, la Inteligencia Artificial explicable, puede interesar a personas con perfiles muy distintos:

• usuarios del modelo, para confiar en él,
• cuerpos regulatorios, para auditarlo,
• usuarios afectados por las decisiones del modelo, para entender su situación y verificarlo,
• data scientists y desarrolladores, para evaluarlo, mejorarlo y explicarlo a sus jefes.

Existen muchos métodos para interpretar un modelo dentro de este campo. Aquí nos centraremos en SHAP, un método basado en la teoría de juegos.

Un desvío por la teoría de juegos, base del método SHAP

El algoritmo SHAP se basa en el método de distribución de riquezas ideado por el matemático y economista Lloyd Shapley. Shapley se preguntó cómo podría repartir las ganancias en un juego cooperativo entre todos los jugadores de forma justa, de modo que cada jugador recibiese una cantidad proporcional a su contribución en el juego.

Vamos a ver un ejemplo de la teoría de juegos: supongamos que Alicia, Borja y Carlos participan en un juego de responder preguntas y que, participando todos juntos, terminan el juego con 900 puntos. Una forma de repartir los puntos sería basándonos en las preguntas que respondió cada uno, pero puede que esto no sea totalmente justo. Por ejemplo, puede que Alicia respondiera una pregunta que también sabía Borja, o también que Carlos supiera la respuesta de una pregunta gracias a un comentario de Alicia.

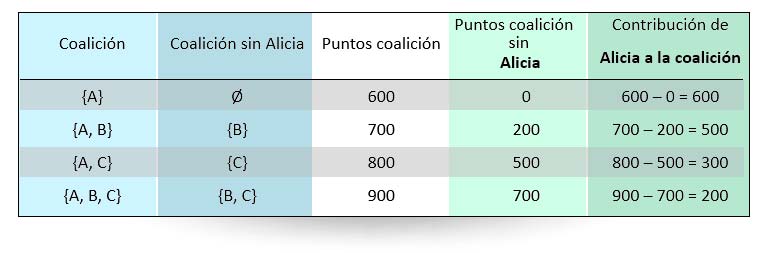
Para ser más justos, tendríamos que comprobar cómo terminaría el juego con todas las posibles coaliciones de jugadores. Pongamos que obtenemos estos resultados: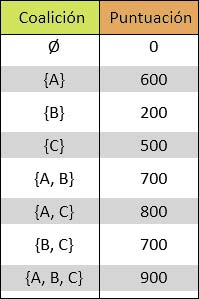

La primera coalición es la vacía, es decir, en la que nadie participa. Esta coalición obtiene, obviamente, 0 puntos. Hay que tener en cuenta que la parte que le tocaría a Alicia no puede depender solamente de la puntuación que obtendría si jugase ella sola, ya que puede que, al colaborar con otro jugador, ambos juntos sean capaces de responder a una pregunta que no habrían sabido de haber jugado por separado.

Shapley definió la contribución de un jugador a una coalición como la puntuación de la coalición completa menos la puntuación de la coalición sin dicho jugador. Por ejemplo, la contribución de Alicia a la coalición formada por Alicia y Borja sería la puntuación de la coalición {A, B} (es decir, 700) menos la puntuación de la coalición sin Alicia (o sea, la puntuación que obtiene Borja solo, que son 200 puntos). Por tanto, la contribución de Alicia a la coalición {A, B} es 700 – 200 = 500 puntos.

Para calcular el valor de un jugador (es decir, la parte que le debería tocar en un reparto justo), hay que tener en cuenta todas las contribuciones a todas las coaliciones posibles que contengan a dicho jugador y hacer una media ponderada de dichas contribuciones. Por ejemplo, para Alicia, podemos obtener la siguiente tabla:

Ahora vamos a hacer varias medias. Primero, agrupamos por el número de integrantes de las coaliciones:

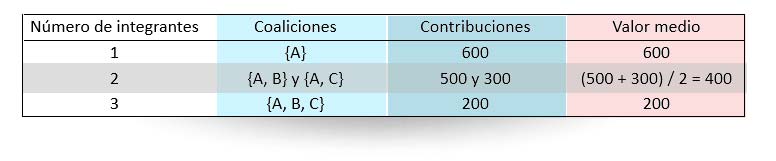En cada fila obtenemos la contribución media de Alicia a coaliciones de 1, 2 y 3 jugadores, respectivamente. Es decir, cuando Alicia participa con otro jugador, de media contribuye 400 puntos, mientras que cuando Alicia participa con otros dos, aporta 200 puntos de media, y, cuando no contribuye con nadie, obtiene 600 puntos.

Finalmente, hallamos la media de estos valores medios, es decir, (600 + 400 + 200) / 3 = 400 puntos. Y esa sería la cantidad de puntos que le corresponderían a Alicia por participar con Borja y Carlos. Si repetimos estos cálculos para Borja y para Carlos, obtenemos que merecen 150 y 350 puntos, respectivamente. Una observación importante es que, si sumamos los puntos repartidos, obtenemos los 900 puntos que ganaron al jugar los tres juntos.

Aplicación del método SHAP en Machine Learning

En el contexto de un modelo de inteligencia artificial, el juego consiste en obtener la predicción del modelo para una instancia concreta y los jugadores son las variables empleadas en dicho modelo. Por ejemplo, supongamos que nuestro modelo predice el salario de una persona en función de su edad, sus años de experiencia y su puesto de trabajo. Para una persona concreta, tendríamos que obtener las predicciones de distintos modelos basados en sólo la edad, sólo los años de experiencia, sólo el puesto de trabajo, la edad y los años de experiencia, la edad y el puesto de trabajo, etc.

Tendríamos que repetir los cálculos de arriba, pero esta vez, en lugar de trabajar con puntos, trabajaríamos con euros. Así, si, por ejemplo, obtenemos los valores -2000, 15000, 25000 para las variables edad, años de experiencia y puesto de trabajo, respectivamente, esto se interpretaría como que, para la persona particular que nos interesa, para la que el modelo ha predicho un salario de 38000 euros, 25000 se deben a su puesto de trabajo, 15000 son por sus años de experiencia, y, debido a su edad, se le han restado 2000 euros a la predicción.

Otras consideraciones del método de explicabilidad SHAP 

¿Y eso es todo? No, eso no es todo. Hay que tener en cuenta que, para tres jugadores, hay que considerar 2³ = 8 coaliciones. O sea que, para 3 variables, hay que entrenar 8 modelos. Y para N variables, 2^N modelos. Esto significa que, si nuestro modelo tuviese 30 variables, tendríamos que entrenar ¡más de 10⁹ modelos! Para que sea factible, hay que aproximar estos valores, eligiendo de forma inteligente las coaliciones o variables que más peso van a tener.

Con estos cálculos y sus aproximaciones pudieron los data scientists de Peter&Wolf identificar, en un tiempo razonable, los problemas de su modelo y construir uno nuevo que funcionó correctamente.

En el Instituto de Ingeniería del Conocimiento (IIC) tenemos una línea de investigación en explicabilidad y, desde hace dos años, hemos aplicado técnicas como esta para depurar y facilitar la puesta en producción de nuestros modelos.