La detección de anomalías tiene como objetivo identificar patrones extraños o atípicos en los datos que generan comportamientos anómalos en los mismos, ya que difieren significativamente del comportamiento de los demás, a los que se los considera como “normales”. En entradas anteriores de este blog ya hemos hablado sobre detección de anomalías en algunos escenarios y proyectos particulares en los que ha trabajado el Instituto de Ingeniería del Conocimiento (IIC), como, por ejemplo, la detección de anomalías en facturas.

En este post haremos primero un repaso de por qué es importante la detección de anomalías y en qué ámbitos pueden ser útiles este tipo de tareas. A continuación, vamos a ver diferentes técnicas que se pueden aplicar para intentar detectar anomalías o outliers, especialmente en datos organizados en formato de series temporales.

Contenido del post Algunas técnicas para la detección de anomalías en series temporales:

• Algunas aplicaciones de la detección de anomalías
• Descomposición de la serie temporal
• Detección de anomalías con el Filtro de Hampel
• Isolation Forest para detectar anomalías en datos
• Detección de anomalías mediante métodos basados en densidad
• Generative Adversarial Networks para la detección de anomalías

Algunas aplicaciones de la detección de anomalías

El desarrollo de la Inteligencia Artificial ha ido tomando mayor importancia en los últimos años y modelos como los orientados al Procesamiento del Lenguaje Natural (PLN) están hoy en día muy de moda. Sin embargo, una de las áreas donde desde hace años que se aplican técnicas de Machine Learning es en la detección de anomalías en los datos. Algunos ejemplos de detección de anomalías son las siguientes:

• Mantenimiento predictivo. En procesos industriales formados por maquinaria sometida a un desgaste, una anomalía en los datos arrojados por los sensores puede ser síntoma de averías y resulta de gran interés para adelantarnos y evitar futuros fallos y problemas. De esta manera, aplicando las medidas de mantenimiento y seguridad requeridas, podemos reducir el tiempo de parada de la cadena de producción y conseguir una reducción de costes.
• Seguridad informática. Se detecta tráfico anómalo para descubrir actividades maliciosas que pueden poner en riesgo los sistemas de una empresa.
• Detección de enfermedades. En el área de salud, se evalúan los signos vitales y otros datos de los pacientes en busca de comportamientos anómalos que pueden ayudar a la detección temprana de enfermedades.
• Detección de bots. En redes sociales, se analizan perfiles cuyo comportamiento puede ser ligeramente diferente al de un humano.
• Análisis de ventas y marketing. Se intentan encontrar patrones no esperados en el comportamiento de los clientes para poder detectar posibles problemas en la cadena de suministro.
• Detección de fraude financiero. Se analizan las transacciones con patrones sensiblemente diferentes a los habituales.

Algunos de estos ejemplos mencionados tienen que ver con datos tabulares tradicionales, otros como, por ejemplo, los del área de salud podrían estar relacionados también con el análisis de radiografías o cualquier otro tipo de imágenes; y, por ejemplo, en el área del mantenimiento predictivo, es muy probable que estemos hablando de datos en formato de serie temporal.

En este post nos vamos a centrar precisamente en la detección de anomalías en series temporales. Una serie temporal es una sucesión de datos ordenados de manera cronológica que se pueden presentar equiespaciados o no temporalmente. Por ejemplo, se mostrarían como series temporales la evolución de la presión de una válvula en una fábrica, la evolución de las acciones de una empresa a lo largo del tiempo, los niveles de contaminación atmosférica, datos de ventas, etc.

Descomposición de la serie temporal

El primer paso para trabajar con este tipo de datos es saber tratar y procesar series temporales. En primer lugar, es importante conocer que una serie temporal se puede descomponer en componentes más básicas para poder entenderla mejor. De esta manera encontramos:

• Tendencia: representa la dirección general o la trayectoria de los datos a largo plazo, ignorando las fluctuaciones a corto plazo. Puede ser creciente, decreciente o constante, además de lineal o no lineal.
• Estacionalidad: muestra los patrones periódicos que se repiten en intervalos regulares a lo largo de toda la muestra. Suelen estar asociados con factores estacionales: meses del año, días de la semana, etc. La estacionalidad puede ser aditiva o multiplicativa.
• Residuos: son aquellas fluctuaciones debidas a la aleatoriedad de los datos que no pueden ser explicadas de otra manera, ni por la tendencia ni por la estacionalidad.

Si tenemos en cuenta esta descomposición de la serie temporal, podemos empezar a identificar qué valores son anómalos haciendo un análisis de la desviación típica de los residuos. En una serie temporal sin anomalías, se espera que sus residuos presenten una distribución normal, con una media próxima a cero, lo que significa que las desviaciones respecto al valor esperado, tanto por encima de su media como por debajo, son igual de probables.

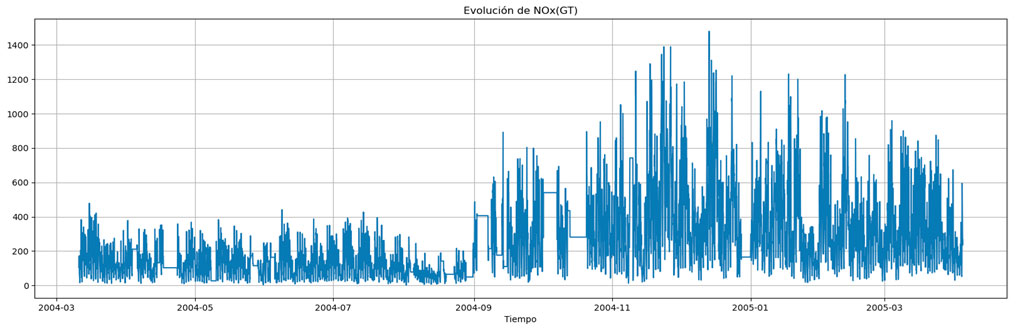
Por ello, podemos establecer un umbral en los residuos, por ejemplo, fijándolo a tres veces la desviación típica, que nos va a permitir afirmar con una confianza significativa que esos valores de la serie temporal son anómalos. Veámoslo con un ejemplo sobre el dataset de Air Quality –disponible en la web del UCI Machine Learning Repository–, tomando una de las variables como sujeto de estudio, en concreto, la variable NOx(GT), que representa la concentración media de partículas de NOx. La serie temporal original es la siguiente:

Ahora vamos a realizar la descomposición de la serie temporal, quedándonos con sus residuos y estableciendo el umbral de tres veces la desviación típica que hemos comentado más arriba.  Obtenemos lo siguiente:

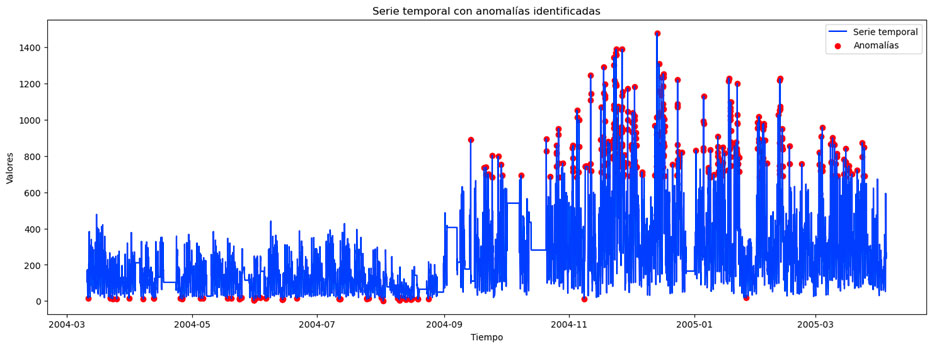
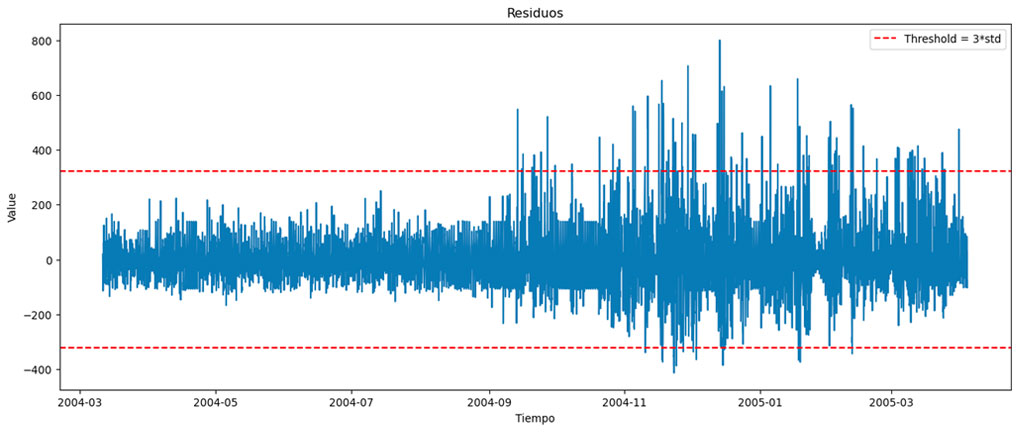Como puede verse, hay ciertos valores que quedan por encima del umbral (marcado por la línea roja discontinua), por lo que podríamos definir a estos valores como valores anómalos. Si lo vemos sobre la serie temporal original, obtenemos lo siguiente:

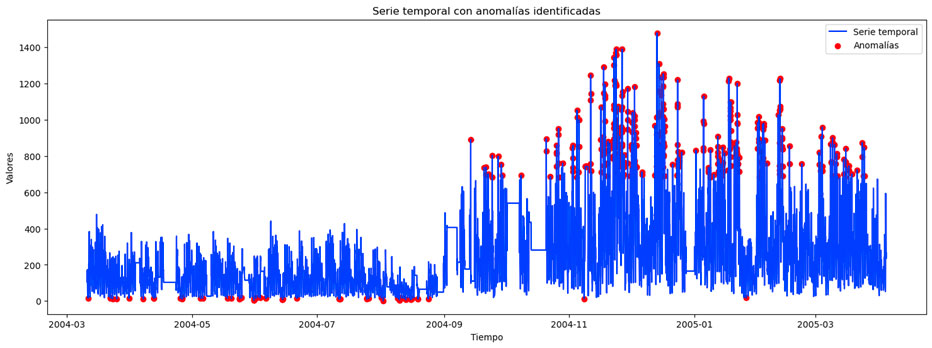Podemos afirmar que este es uno de los métodos más simples para detectar anomalías en series temporales y su interpretación es bastante intuitiva. Sin embargo, también presenta algunos inconvenientes importantes como que no tiene en consideración dependencias temporales complejas, ya que se asume que cada punto es independiente. Además, el umbral fijado puede ser algo subjetivo y dependiente del problema.

Por poner un ejemplo para entender esta selección subjetiva del umbral: en este caso, estamos hablando de un gas emitido a la atmósfera, sobre el cual es posible que existan estudios que indiquen cómo influye en la salud de las personas o cómo afecta a la flora y fauna local. Así, podríamos concluir que quizás este umbral, aunque pueda estar bien elegido desde el punto de vista estadístico, no es el mejor umbral posible, ya que deberíamos seleccionar aquel que nos resulte de mayor interés en nuestro análisis.

Aunque en este ejemplo puede entenderse de manera clara este hecho, en otros casos de uso, la ausencia de un conocimiento experto sobre el proceso del que tratan los datos puede llevarnos a utilizar el criterio estadístico en la selección del umbral y este no representar la mejor opción.

Detección de anomalías con el Filtro de Hampel 

Tras una primera aproximación a la serie temporal, una de las técnicas que se puede aplicar a la detección de anomalías en datos de este tipo es el filtro de Hampel, que consiste en establecer una ventana de datos sobre la cual se calculará la mediana. Por tanto, en este caso, es recomendable tomar un valor impar para facilitar ese cálculo, aunque, obviamente, se puede tomar cualquier valor. Después, se calcularía la desviación típica de cada muestra respecto al valor de la mediana. Esto se conoce como MAD (del inglés, Median Absolute Deviation).

Tras esto, se multiplica por un factor para que sea un estimador consistente. Este factor es aproximadamente 1.4826 para una distribución Gaussiana. Por último, se multiplica por el número de sigmas que queramos para asegurar que sea un outlier.

MAD = median(| |)

Threshold = n * σ * 1.4826 * MAD

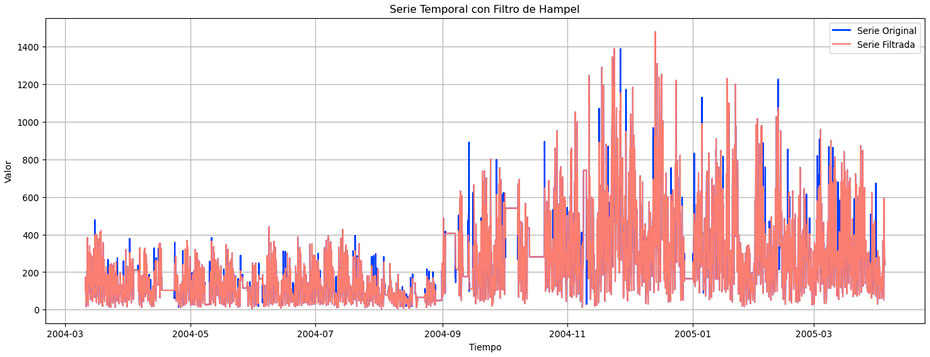
Si un valor supera este threshold, se sustituye este valor por el valor de la mediana en dicha ventana. Aplicando esto en Python, obtendríamos la siguiente gráfica. Se puede ver que la serie filtrada es más “suave” (alcanza picos menores) que la serie original.

Isolation Forest para detectar anomalías en datos

Uno de los algoritmos más empleados para la detección de anomalías es Isolation Forest. Este es un algoritmo no supervisado que utiliza árboles binarios para aislar las muestras. En esencia, el algoritmo funciona de la siguiente manera:

• Se toma un valor aleatorio dentro del rango de valores de la variable a estudiar.
• Se hace una división por dicho valor, de esta forma se crea un nuevo nodo.
• Se va repitiendo esto hasta que cada punto esté aislado en un único nodo.

Una vez que se ha realizado esto, se le asigna una puntuación a cada una de las muestras teniendo en cuenta el número de divisiones necesarias para aislar el punto. De esta manera, cuantas menos divisiones se necesiten para aislar un punto será porque más anómalo es, ya que es un valor claramente diferenciable de los demás. A continuación, se presenta una imagen con el objetivo de ejemplificar de manera sencilla el funcionamiento de Isolation Forest: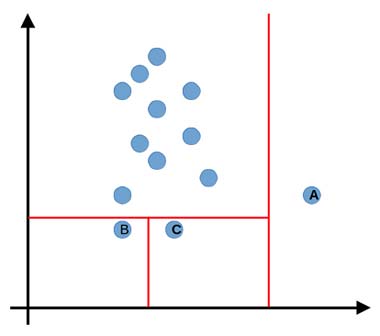

En la imagen anterior vemos que para aislar el punto A es suficiente con una única división (en este caso, vertical), por lo que, más tarde, tendrá una puntuación que indicará claramente que es un outlier. Sin embargo, en el caso de los puntos B y C, se necesita una división extra para aislarlos, con lo que irá disminuyendo la probabilidad de que estos puntos sean outliers. Hay que tener en cuenta que en la imagen sólo se han realizado tres divisiones con el objetivo de facilitar la explicación, pero el algoritmo continuaría haciendo divisiones hasta que todas las muestras quedasen aisladas.

Este algoritmo se encuentra implementado en Sklearn, una de las librerías más famosas de Machine Learning para datos tabulares con Python. Así, aplicándolo sobre nuestros datos, podemos llegar a lo siguiente:

Isolation Forest es un algoritmo muy eficiente, de complejidad lineal, que nos va a permitir trabajar con grandes cantidades de datos y con un gran número de variables. Sin embargo, hay que tener en cuenta que Isolation Forest, como otros métodos basados en conjuntos o ensembles de modelos, presenta una serie de hiperparámetros que deberemos ajustar de la manera más adecuada posible y que cuya elección puede afectar sensiblemente a los outliers señalados por el algoritmo. Además, debemos recordar que es un algoritmo no supervisado, por lo que pueden aparecer falsos positivos que debamos analizar posteriormente en detalle.

 

Detección de anomalías mediante métodos basados en densidad

Otra opción para detectar anomalías en series temporales es hacer uso de métodos basados en densidad, como, por ejemplo, DBSCAN (Density-based spatial clustering of applications with noise). Se trata de un algoritmo de agrupamiento no supervisado que, aunque en origen no fue diseñado para solventar este tipo de tareas, puede ayudarnos en la búsqueda de anomalías.

En concreto, DBSCAN encuentra el número de clústeres en los datos sin necesidad de prefijar una cantidad de manera manual. Además, es resistente al ruido y puede identificar aquellos puntos que no pertenecen a ningún clúster en específico y que podrían ser outliers.

DBSCAN se basa en dos parámetros principales para construir toda su lógica:

• Epsilon hace referencia al radio de búsqueda o distancia a la cual deben encontrarse un punto de otro para que pertenezcan al mismo clúster.
• MinPts es el número mínimo de puntos que deben existir dentro del radio definido por Epsilon para que un punto sea considerado punto central, que son los esenciales para la formación de un clúster.

El algoritmo funciona, de manera algo simplificada, como sigue:

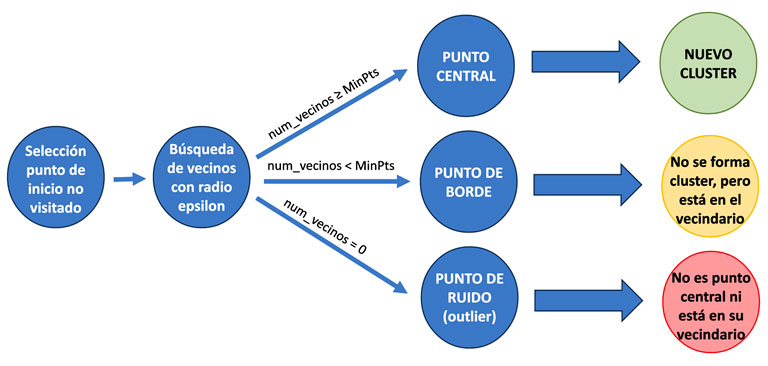Tras analizar el funcionamiento de DBSCAN, podemos utilizarlo para detectar anomalías en series temporales quedándonos con esos puntos que el algoritmo identifica como puntos de ruido (outliers). Así, aplicando DBSCAN sobre los datos que venimos analizando, obtenemos el siguiente gráfico:

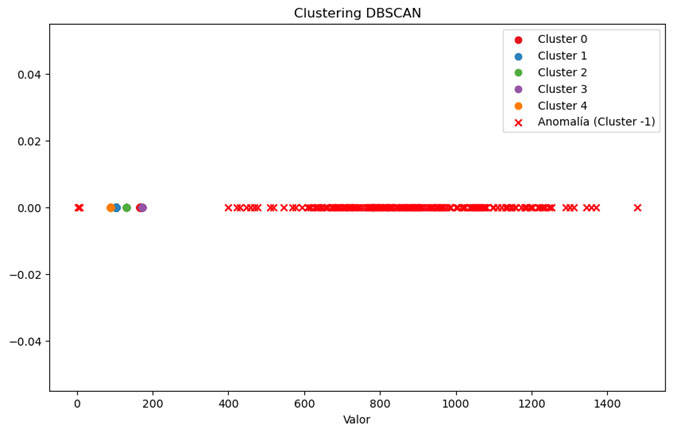En este caso, al tener una única dimensión, ya que tenemos sólo una variable, este gráfico no es tan visual como en el caso de tener varias variables. Sin embargo, se puede ver que el algoritmo ha encontrado 5 clústeres y los demás puntos han sido marcados como anomalías. Si recuperamos la forma temporal de los datos y pintamos las anomalías sobre el gráfico, obtenemos lo siguiente:

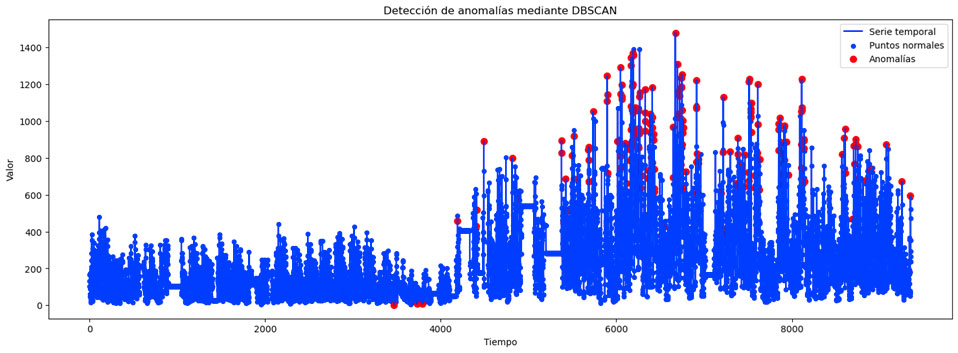En el caso de DBSCAN encontramos ciertas ventajas al ser un algoritmo de aprendizaje no supervisado: no requiere prefijar el número de clústeres y es capaz de funcionar con datos que están aleatoriamente distribuidos. Sin embargo, también es bastante sensible al valor de sus parámetros Epsilon y MinPts y le es complicado encontrar los clústeres si la densidad de los datos varía o si disponemos de pocas muestras en nuestro dataset.

 

Generative Adversarial Networks para la detección de anomalías

Otra posibilidad para encontrar anomalías en series temporales que abandona los enfoques más tradicionales es hacer uso de las redes GAN (Generative Adversarial Networks), que normalmente se aplican en la generación de imágenes y de datos sintéticos. Recordemos primero cómo funciona una red GAN.

Descritas en el año 2014 por Ian Goodfellow, las Redes Generativas Antagónicas (en su traducción al castellano), están formadas por una red neuronal conocida como generador, que se encarga de producir nuevos datos con una distribución similar a los datos con los que fue alimentado, y por otra red conocida como discriminador, que intenta descubrir si los datos producidos por el generador pertenecen a la muestra original o son nuevos. De esta manera, ambas redes se enfrentan para que, a medida que el discriminador va mejorando y es capaz de detectar con mayor precisión si los datos son falsos, el generador va perfeccionándose para conseguir cada vez unos datos a su salida lo más parecidos posible a la distribución original.

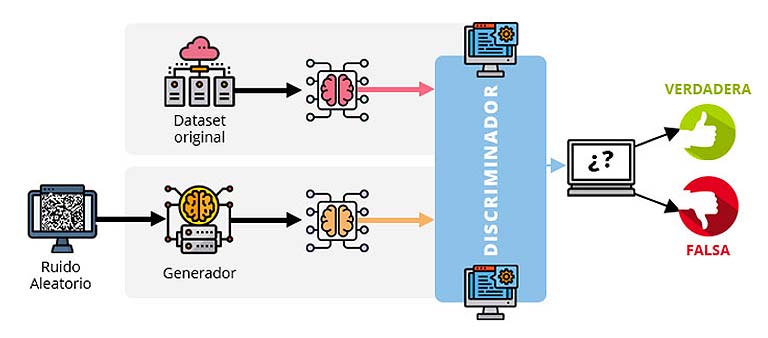
Un ámbito donde se aplica y entiende muy bien el funcionamiento de este tipo de redes es el del tratamiento de imágenes. Por ejemplo, para el caso de uso de generación de rostros de personas, la red generadora produce imágenes de caras de personas y la red discriminadora tiene que descubrir si es un rostro real o no. De esta manera ambas redes van compitiendo de tal manera que el generador acaba siendo capaz de producir imágenes muy realistas.

Este concepto podría ser llevado a la detección de anomalías en series temporales y, de hecho, existen algunos papers en relación a esto con modificaciones de las redes tipo GAN (TadGAN [1]) para intentar descubrir qué datos de una serie temporal deberían ser considerados como anomalías. Por lo general, el enfoque para abordar este tipo de problemas consiste en entrenar primero la red sobre los datos sin anomalías. De esta manera, la red es capaz de aprender la distribución habitual de los datos y, así, el discriminador aprenderá a identificar datos considerados como normales. Posteriormente, cuando empiecen a llegar datos con anomalías, la red será capaz de reconocerlos como datos anómalos.

Si aplicamos el enfoque de la GAN sobre nuestros datos, obtenemos lo siguiente:

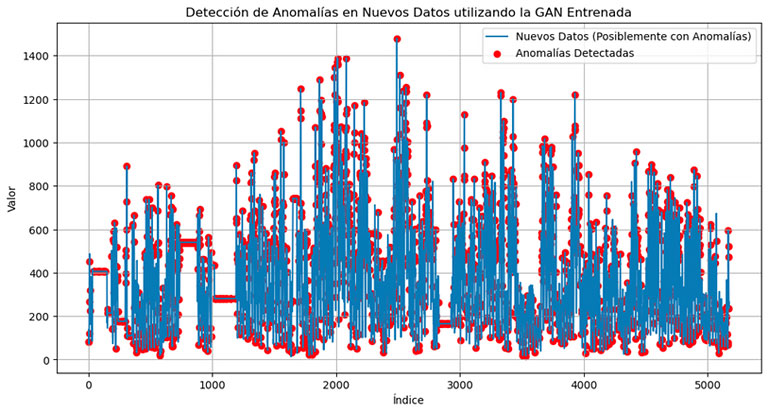Para empezar, hay que destacar que hemos tenido que dividir la serie temporal en dos: un conjunto de entrenamiento en el que hemos supuesto –de manera visual o con alguno de los métodos anteriormente explicados– que no existen anomalías y otro conjunto de prueba, para que la red encuentre los datos anómalos. Como vemos, en este caso, encuentra quizá demasiados datos anómalos, y es que existen varias limitaciones en este tipo de modelos.

Por una parte, aunque es un método no supervisado, sí que sería importante conocer con seguridad que los datos que le damos para entrenar no contienen anomalías. En este ejemplo, hemos asumido que una parte de los datos no tenía anomalías, lo cual puede ser totalmente falso.

Por otra parte, estamos ante un modelo de Deep Learning y, como es habitual, son modelos que necesitan de una cantidad de datos superior a los modelos tradicionales para ser capaces de aprender. Además, a esto habría que sumarle la necesidad de realizar un estudio detallado de la arquitectura de la red, ajustar el número de neuronas, ajustar el learning rate cuidadosamente… En general, hay que tener en cuenta todos esos aspectos que conciernen a un modelo de este tipo y que son fundamentales para obtener un buen rendimiento de ellos.

En este post hemos visto por qué es importante detectar anomalías en series temporales y algunos de los métodos que podemos aplicar y que los profesionales del IIC utilizan cuando se tienen que enfrentar a este tipo de tareas. ¿Conocías todos estos métodos? ¡Esperamos que puedas aplicar las nuevas ideas a tus proyectos!