Organizar turnos de trabajo, planificar viajes de transportistas o descubrir nuevos materiales. Enviar sondas al espacio, planear las trayectorias y también hacer comprobaciones del tipo: si el componente A falla, pero B sigue funcionando, entonces, ¿seguirá funcionando la sonda? Todas estas tareas tienen algo en común: se pueden plantear como un problema matemático de optimización, en el que se busca una configuración adecuada con la que una función alcanza su valor máximo o mínimo.
Estos problemas de optimización no son exclusivos del ser humano. De hecho, la naturaleza ha estado resolviendo problemas de optimización mucho antes de que existiéramos, y lo hace mucho mejor que nosotros. Por ejemplo, las pompas de jabón son esféricas porque, de todas las superficies que encierran el mismo volumen, la esfera es la menor. Los rayos buscan el camino de mínima resistencia hasta el suelo, y, aunque los ríos del Amazonas parecen seguir caminos aleatorios, realmente están buscando también el camino más fácil hasta el océano.
Es posible usar la Física para resolver problemas de optimización. Por ejemplo, se puede encontrar la salida de un laberinto en milésimas de segundo usando helio en estado de plasma. También se ha empleado la Física para diseñar cubiertas de edificios, doblando un alambre con la forma de la parte superior de las paredes y sumergiéndolo en agua con jabón. Se obtiene así la superficie mínima con los límites dados:
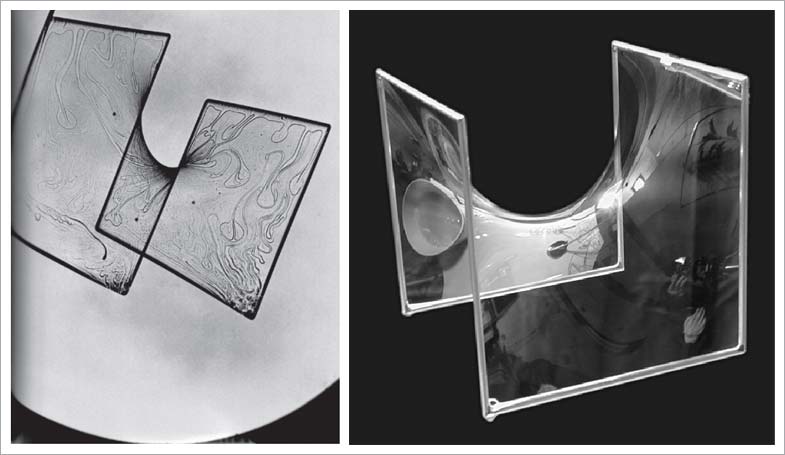
Fuente: http://ojs.redfundamentos.com/index.php/rita/article/view/107/107, https://www.researchgate.net/profile/Alessandra-Capanna/publication/264238453/figure/fig2/AS:392400829730827@1470567056696/Basento-river-soap-blow-bubble-check-it-is-the-minimal-surface-set-from-this-peculiar.png
Precisamente en la Física se basan algunas de las técnicas cuánticas que están surgiendo y que prometen resolver problemas de optimización más rápido que los computadores clásicos. Hasta que se construya un computador cuántico con capacidad suficiente para problemas grandes, como veremos, la técnica que se suele emplear consiste en combinar recursos cuánticos y clásicos.
Técnicas clásicas de optimización
Para resolver problemas de optimización en un ordenador clásico, existen dos tipos de algoritmos: los algoritmos exactos y las heurísticas.
Los algoritmos exactos recorren todas las posibles soluciones, descartando de una forma más o menos inteligente algunas que no pueden ser óptimas. Con estas técnicas se puede hallar la solución óptima de forma garantizada. No obstante, son poco eficientes. Pensemos, por ejemplo, en el problema del viajante, que consiste en hallar el camino más corto que visita los puntos deseados: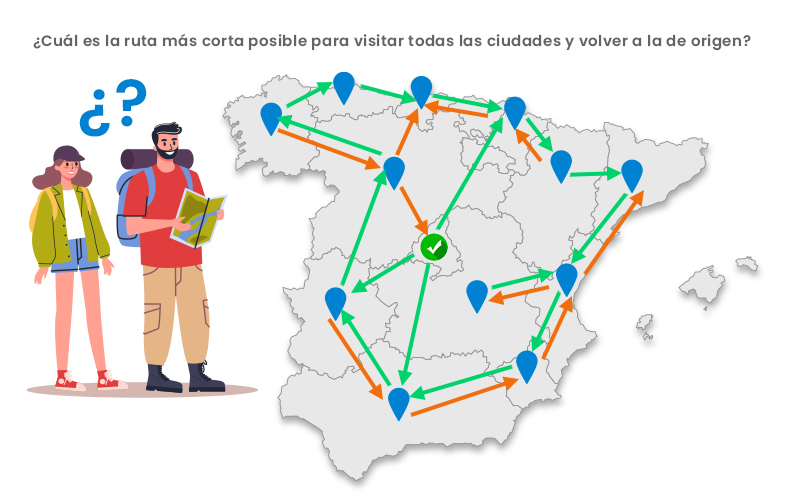
Este problema es sencillo de plantear, pero difícil de resolver: hay (N − 1)!/2 soluciones posibles para N ciudades. Esto significa que el número de caminos posibles entre los que tendríamos que buscar crece como en la siguiente tabla:
| N | Número de caminos |
| 5 | 12 |
| 10 | 181440 |
| 15 | 4,36⋅1010 |
| 20 | 6,08⋅1016 |
| 61 | 4,16⋅1081 |
| 62 | 2,54⋅1083 |
Se estima que hay entre 1078 y 1082 átomos en el Universo observable, por lo que el problema del viajante para 62 ciudades tiene más soluciones posibles que átomos en el Universo. Los mejores algoritmos exactos, que descartan algunas configuraciones antes de examinarlas, resuelven este problema en tiempo exponencial.
Las heurísticas son mucho más rápidas encontrando una solución, aunque esta puede no ser óptima. Estos métodos encuentran una solución del problema de optimización y la van mejorando iterativamente. Dado que los métodos exactos son tan ineficientes, se suelen emplear las heurísticas más a menudo. Para dar la mejor solución posible, se suelen ejecutar muchas veces con condiciones iniciales distintas.
El potencial de la computación cuántica
Con la introducción de los computadores cuánticos, se descubrieron nuevas técnicas para resolver gran variedad de problemas, al menos de forma teórica, como se describe en este post sobre el potencial de la computación cuántica. Estos computadores controlan y manipulan la evolución de los estados cuánticos a lo largo del tiempo para hacer los cálculos necesarios, y es precisamente gracias a este control que se pueden resolver tantos problemas distintos.
Existe una familia de computadores cuánticos que son menos ambiciosos, ya que solo pretenden realizar una tarea: resolver problemas de optimización. Estos computadores aprovechan la evolución natural de los estados cuánticos en lugar de intentar controlarla. Dicho con otras palabras, usan la Física para resolver problemas de optimización. Esta técnica se llama el temple cuántico.
Estos computadores contienen una rejilla de pequeños anillos, los qubits o bits cuánticos, que están hechos de un material que muestra efectos cuánticos por debajo de los 9,2 grados Kelvin. Entre otras cosas, una de las propiedades que tienen los qubits a estas temperaturas es que se pueden encontrar en estado de superposición: a diferencia de los bits, que solo pueden estar en estado 0 ó 1, los qubits se pueden encontrar en estado mixto de 0 y 1 y solo se definen cuando se observan.
Técnicas cuánticas para la optimización
Gracias a la técnica del temple cuántico, podemos usar la Física para resolver problemas de optimización sin recurrir a un alambre y agua con jabón. Una parte fundamental de la Física es que todo tiende a su estado de mínima energía: los objetos se deslizan por las rampas, todo aquello que está caliente se enfría, etc. Esto también es cierto en el mundo cuántico.
Con esta técnica, aprovechamos la evolución natural de los estados cuánticos para minimizar la energía. Empezamos con unos qubits en estado de superposición, es decir, en estado 0 y 1 al mismo tiempo. Los situamos en un estado energético concreto por medio de campos magnéticos y los entrelazamos de manera adecuada para reflejar, mediante su estado energético, el problema de optimización. Dejamos que la Física actúe y busque el estado de mínima energía, del mismo modo que cuando dejamos un objeto en la parte superior de una rampa, este busca el estado de mínima energía deslizándose hacia abajo. Al dejar actuar a la Física, se modifican las probabilidades de que cada qubit termine en un estado 0 ó 1 cuando este sea observado. Al final del proceso, cada qubit adopta el estado 0 ó 1, encontrándose el conjunto en un estado de menor energía, o uno muy cercano al mínimo. La configuración final corresponde a la solución buscada.
Cuándo jugar con pompas de jabón cuánticas
Si el problema de optimización es demasiado grande para los computadores cuánticos que hay hoy en día, se pueden aplicar algoritmos híbridos, que combinan recursos clásicos con recursos cuánticos. Generalmente, esta cooperación consiste en usar primero algoritmos clásicos para descomponer el problema en partes y, a continuación, en enviar esas partes más pequeñas al computador cuántico, para finalmente combinar las soluciones.
Esta técnica se ha empleado ya para resolver problemas reales. Por ejemplo, Volkswagen la ha aplicado para decidir de qué color debe ser la base de pintura de las piezas de carrocería que van pasando por la cinta. También en el mundo de la banca se ha hecho uso de esta colaboración para optimizar carteras de inversión.
¿Cuándo utilizar la computación cuántica? Como siempre, es necesario estudiar qué recursos son necesarios. Hay problemas que tienen una estructura tan sencilla que no es necesario recurrir a un computador cuántico, y hay otros que son tan complejos que no hay forma eficaz de descomponerlos para que los resuelva un computador cuántico.
Entre las actividades de investigación del Instituto de Ingeniería del Conocimiento (IIC), contamos con una línea de observación de los avances en la computación cuántica, con el fin de poder incorporar esta tecnología a nuestros servicios en cuanto aporte ventajas de negocio.
