Desde hace unas décadas, el campo de las redes neuronales ha avanzado enormemente. Comenzando en el año 1958 con el Perceptrón Simple de Frank Rosenblatt, y superando progresivamente las limitaciones encontradas en cada paso evolutivo de este tipo de algoritmos de aprendizaje. Hoy en día, el campo del aprendizaje profundo vive una época de auténtico esplendor. Esto ha quedado patente gracias al desarrollo, por ejemplo, de los grandes modelos de lenguaje (large language models, LLMs) a cuyo uso estamos tan acostumbrados actualmente.
Sin embargo, a pesar de sus capacidades, los modelos de lenguaje actuales basados en redes neuronales presentan aún importantes limitaciones:

- Las ingentes cantidades de datos requeridas para su entrenamiento.
- Su comportamiento en muchas ocasiones de tipo “caja negra” en los que es muy difícil, por no decir imposible, obtener una explicación de por qué están dando una determinada salida u otra.
- Su falta de generalización en dominios diferentes al que han sido entrenados.
Debido a estos y otros motivos, parte de la comunidad científica e investigadora está en busca de nuevas vías de mejora para los modelos de lenguaje actuales. El objetivo es que estos modelos puedan superar las limitaciones existentes y conseguir nuevos paradigmas más eficientes, justos y responsables.
En este contexto es donde surgen las Redes Kolmogorov-Arnold (KAN – Kolmogorov-Arnold Networks) como una propuesta alternativa e innovadora. Aunque en realidad no son un concepto actual, fueron propuestas de nuevo en el paper “KAN: Kolmogorov-Arnold Networks”).
Antecedentes: el perceptrón multicapa
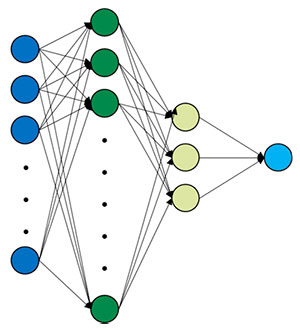
La mayoría de las arquitecturas actuales implementan los Perceptrones Multicapa (MLP), al menos en alguna parte de su arquitectura. Estas son un tipo de redes neuronales que surgieron como evolución del Perceptrón Simple y que están compuestas por neuronas totalmente conectadas entre ellas. Este tipo de redes neuronales se fundamenta en el Teorema de Aproximación Universal que establece que una red neuronal con una sola capa oculta (aunque con un número suficiente de neuronas) y una función de activación no lineal puede aproximar cualquier función continua.
Sin embargo, y como cabría esperar, a pesar de este poder teórico, el Teorema de Aproximación Universal no garantiza que:
- Encontrar los pesos óptimos (es decir, entrenar la red) sea una tarea sencilla.
- Sea eficiente en términos de cómputo o memoria.
- Generalice bien.
En un MLP, el algoritmo con el que realmente aprende la red, conocido como algoritmo de backpropagation, tiene como objetivo encontrar los pesos óptimos de la red que permitan reducir lo máximo posible el error de predicción. De manera sencilla, estos pesos son números que determinan qué tan importante es cada entrada para predecir la salida. Así, durante el entrenamiento, la red ajusta estos pesos para que sus respuestas se acerquen a las respuestas correctas.
Por otra parte, cada salida de cada una de las neuronas se hace pasar posteriormente por una función de activación (no lineal, para poder resolver problemas complejos). Esta función de activación decide cuánto se “activa” una neurona después de recibir sus entradas y pesos.
Resumiendo, en un MLP se tienen las siguientes entidades:
- Entradas de la red: se corresponden con las variables de nuestro problema (por ejemplo, el tamaño en metros cuadrados de una casa, el número de habitaciones, el número de cuartos de baño…)
- Pesos de la red: es lo que se aprende durante el entrenamiento e indica cuánta importancia tiene cada entrada en cada neurona.
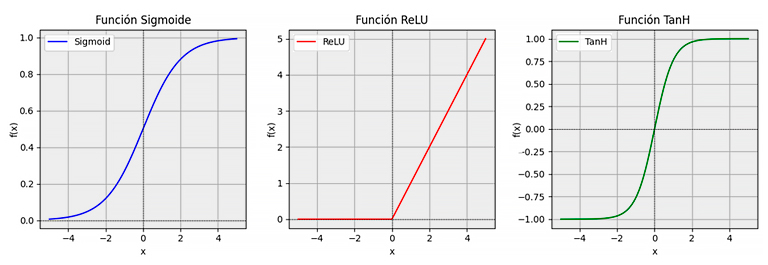
- Función de activación: decide si se activa la neurona y cuánto. Estas funciones ϕ_(q,p) y Φ_q son fijas, es decir, se eligen durante el proceso de diseño de la red. Una de las más utilizada es la función ReLU (Rectified Linear Unit).
- Salidas: se corresponden con las predicciones del modelo.
Un nuevo enfoque: las Redes Kolmogorov-Arnold
Sin embargo, el enfoque de las Redes Kolmogorov-Arnold es distinto. Estas se encuentran respaldadas por el Teorema de Representación de Kolmogorov-Arnold que establece que cualquier función multivariante puede ser expresada como una composición finita de funciones continuas de una única variable combinadas con la operación suma.
Pongamos esto en términos más sencillos. Imagina que queremos hacer una pizza. Ya que vamos a ponernos a ello, propongámonos un objetivo sencillo: ¡conseguir la mejor pizza del mundo!
Antes este gran reto, lo mejor es descomponer la tarea en tareas individuales más sencillas. Podemos decir que cocinar la mejor pizza del mundo se compone de:
- Conseguir la mejor masa del mundo.
- Conseguir la mejor salsa del mundo.
- Conseguir el mejor queso del mundo.
- Conseguir el resto de los ingredientes… también los mejores del mundo.
Empecemos entonces con el primer paso:
- La masa: importante cómo está amasada, tiempo de cocción, la harina…
- La salsa: es clave su sabor, por lo que hay que elegir unos buenos tomates, una cantidad equilibrada de especias, jugar con las proporciones…
- El queso: importante elegir el tipo de queso, así como la cantidad empleada y conocer bien cómo se derrite para obtener óptimos resultados.
- Los ingredientes adicionales: si va a llevar carne, hay que prestar atención a la calidad.
Si seguimos estos pasos, estaremos haciendo una pizza al famoso estilo Teorema de Representación de Kolmgorov-Arnold, o lo que es lo mismo, estamos descomponiendo una función de múltiples variables (la pizza entera) en una suma de funciones univariantes (ajustar cada componente de la pizza por separado).
Expresado de forma más matemática tendríamos lo siguiente:

Esta es, precisamente, la ecuación del Teorema de Representación de Kolmogorov-Arnold. Aquí es donde surge la diferencia clave de las KAN respecto a los MLPs. Estas funciones ϕ_(q,p) y Φ_q son las que va a aprender la red durante el proceso de entrenamiento. En lugar de ser funciones como la ReLU, mencionada anteriormente, son funciones B-Splines.
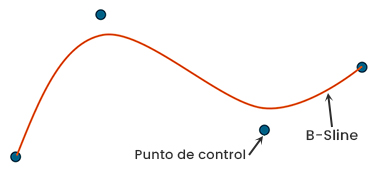
Las funciones Spline, en general, son funciones compuestas por varios polinomios que se unen suavemente en ciertos puntos llamados nodos o puntos de ruptura. Las B-Spline, por su parte, son una variedad de Spline que utiliza puntos de control para ajustarse mejor a los datos de tal manera que no sobreajustan ni subajustan a estos y, así, se pueden adaptar a cambios en los datos sin ajustar de nuevo todo el modelo.
Por tanto, la KAN va a tener que aprender a encontrar estos puntos de control durante el proceso de entrenamiento. Así, una red KAN general es una composición de 𝐿 capas, donde la salida de la KAN resulta en:
KAN(x)=(Φ_(L-1)∘Φ_(L-2)∘…∘Φ_1∘Φ_0 )x
La función KAN(x) se obtiene aplicando múltiples transformaciones sucesivas a con cada capa
- x: Es la entrada de la red.
- Φ_0(x): Es la primera transformación univariante aplicada a la entrada .
- Φ_1(·): Aplica otra transformación univariante a la salida de .
- Φ_2(·): Aplica otra transformación univariante a la salida de .
- …
- Φ_(L-1): Es la última transformación antes de la salida final de la red.
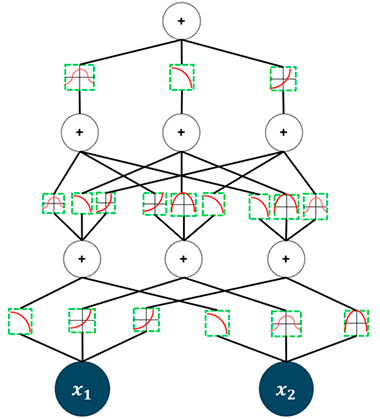
De esta manera, la arquitectura de una KAN quedaría como en la siguiente imagen:
Por tanto, las funciones de activación que se aprenden se encuentran en las aristas, mientras que en los nodos se realiza la operación suma, a diferencia de en los MLPs en los cuales, los pesos, que se aprenden, se encuentran en las aristas y las funciones de activación que son fijas y no se aprenden, se encontrarían en los nodos.
Se pueden resumir las diferencias y similitudes entre los MLPs y las KAN como sigue:
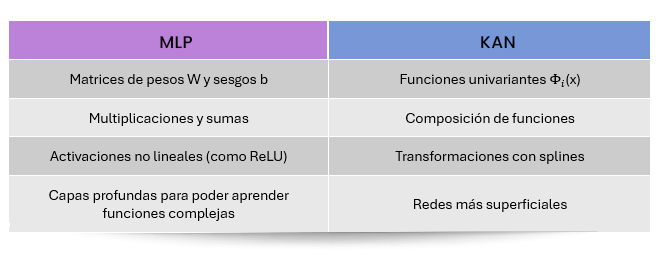
Tabla 1 – Comparativa MLP vs KAN
Los autores del paper mencionado al comienzo concluyen estas gráficas tras analizar el rendimiento de las KAN frente a los MLPs para aprender funciones:
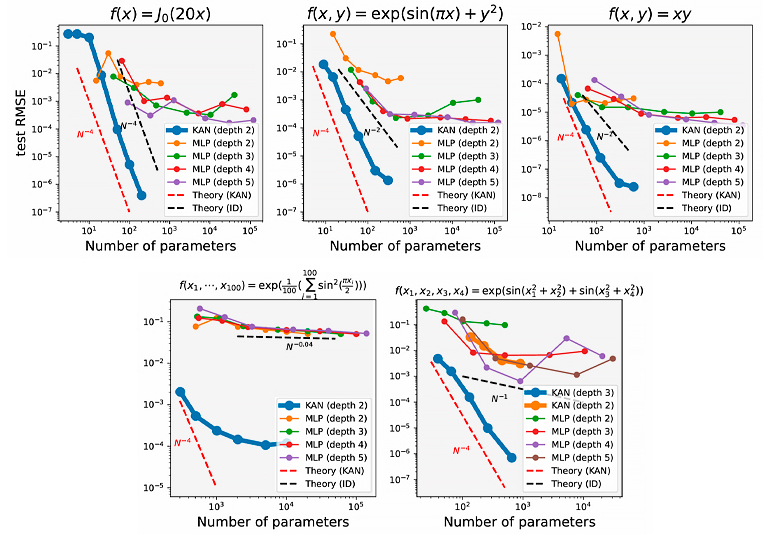
Ilustración 5 – Comparativa número de parámetros y error MLP vs KAN (Fuente: paper KAN: Kolmogorov-Arnold Networks)
Aquí se puede ver que, de manera general, el número de parámetros necesarios para resolver un problema mediante una KAN es menor que en el caso de los MLPs, por lo que son más eficientes.
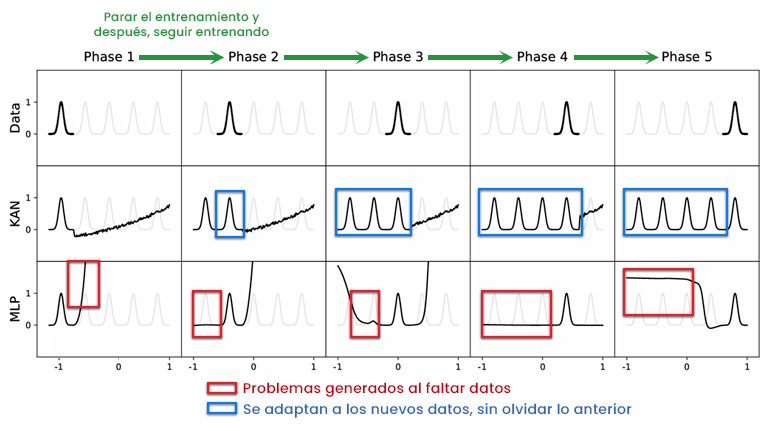
Además, las KAN parecen presentar una capacidad natural para no olvidar lo aprendido en etapas anteriores como puede verse en la siguiente imagen:
Esto podría deberse a que al recibir nuevos datos las B-Splines, sólo ajustan los puntos de control relativos a esos nuevos datos, por lo que permanecen inalterados los anteriores y el modelo “retiene” el aprendizaje.
La explicabilidad como pilar fundamental de los modelos
Por último, pero no menos importante, se mencionó anteriormente que una de las limitaciones de los MLPs residía en su comportamiento del tipo modelo de “caja negra” donde, una vez que los datos se pasaban a lo largo de la red, no se es capaz de conocer porqué el modelo ha decidido sacar una salida y no otra.
 Por su parte, las KAN permiten expresar su salida en lo que se conoce como “función simbólica” que describe cómo la red transforma una entrada en una salida expresando todas las funciones internas de forma transparente y legible.
Por su parte, las KAN permiten expresar su salida en lo que se conoce como “función simbólica” que describe cómo la red transforma una entrada en una salida expresando todas las funciones internas de forma transparente y legible.
De esta manera, la red nos da una ecuación matemática, es decir, la expresión con la que podríamos calcular los valores resultados. Esto es de gran interés en algunos ámbitos, primero porque permite ver cómo afecta cada variable a la salida, pero también porque permite extraer leyes o fórmulas subyacentes en los datos experimentales y ayudar en la justificación y toma de decisiones.
No obstante, las KAN no son perfectas. Se puede observar que este tipo de redes, al menos en el estado del arte actual, aunque pueden ser capaces de resolver un problema con menos capas que las necesarias en el caso de los MLPs, su proceso de entrenamiento puede resultar mucho más lento.
Sin embargo, existe una amplia comunidad de investigación en este tipo de arquitecturas, que está trabajando en superar las limitaciones existentes y en ampliar su rango de aplicabilidad a otros ámbitos. Por ejemplo, en este repositorio existe un recopilatorio de proyectos que están siendo actualmente desarrollados haciendo uso de KAN donde se puede ver un gran número de proyectos en marcha.
En resumen, las redes KAN se posicionan como un nuevo paradigma que puede solventar las limitaciones de los modelos de lenguaje tradicionales basados en variantes de los perceptrones multicapa. Así, este tipo de redes al ser más sencillas, contando con un menor número de parámetros, pueden permitir entrenamientos más rápidos y eficientes. Además, la explicabilidad resulta de manera natural en su implementación, por lo que dan lugar a modelos más transparentes de cara al usuario o cliente a la vez que permiten extraer mayor valor al desarrollador o investigador.